Atcoder 练习

ARC072

在一个数轴上给定初始位置和结束位置的距离，给定一长度为 $n$ 的序列 $d$ , 每次朝目标的方向走，如果可以使距离变小，就走，反之则原地不动。有 $Q$ 次询问，每次询问修改某一个 $d_i$ 后人是否能到达终点。

$n,Q \leq 5 \times 10^5$

考虑每次修改后如何判断其是否能到达终点，有两点限制：

那么可以设 $f_i$ 为 $[0,i)$ 这些操作后中的距离值，$g_i$ 为在保证 $(i,n]$ 操作后成功的条件下距离最小值。

则 $\text{ans}_i=[[g_i,f_i]\neq\phi]$

在一个平面直角坐标系中，给定 $n$ 对点，坐标 $(r,c)$ 为整数，且 $r\in [0,R],c\in [0,C]$，保证没有重点，判断是否能在连线不相交的情况下连起所有点对。

$R,C\leq10^8,n\leq10^5$

发现只有两点都在边界上的情况下才会改变连通性，问题就变成了判断边界上的点对之间的连线是否相交。

把四条边放到数轴上其实就是个括号匹配合法性问题，用 set 存一下，然后 stack 判断。

给定一张 $n$ 个点 $m$ 条边的带权无向图和图上的源点 $S$ 和汇点 $T$ . 现在有两个人分别从 $S,T$ 出发，到对方的点，途中只走最短路径，求可能的不相遇（在同一点或同一边相遇都算）的路径方案数。

$n\leq10^5,m\leq2\times10^5$

不相交这一条件不太好处理，考虑先统计出所有路径方案数，再减去相交的情况。

统计所有方案数的时候只需要在最短路求的时候 DP 一下即可，记录从 $S$ 点出发的路径距离 $d_S$ 和方案数 $f_S$ ，同理记录 $d_T,f_T$ . 那么总的方案数就是 $f_S[T]^2$

主要问题在于计算相交的方案数，我们分点相交和边相交统计：

对于每个 $d_S[u]=d_T[u]$ 的点 $u$ , 对答案做出 $f_S[u]f_T[u]$ 的贡献。
对于每个 $d_S[u],d_T[u]<\frac{d_S[T]}{2}$ 且 $d_S[u]+d_T[v]+w_{u,v}=d_S[T]$ 的边 $(u,v)$ , 对答案做出 $f_S[u]^2f_T[v]^2$ .

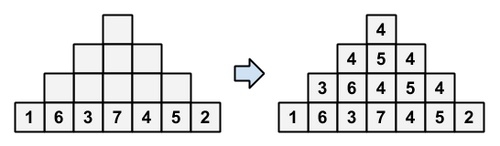
一个金字塔，共有 $n$ 层，金字塔的最底层是一个 $1$ 到 $2n-1$ 的排列，已知这个排列。
除最底层以外，金字塔的每个格的数是下一层中它左下方、正下方、右下方这3个数的中位数。
求塔顶的数。

$n\leq10^5$

关键是如何利用中位数的性质，中位数取值看的是大小关系，于是我们考虑二分答案，每次看是否符合条件。

每次判断答案是否大于 $\text{mid}$ , 记 $\geq mid$ 的数为 $1$ , $<mid$ 的数为 $0$ ，分两种情况：

数轴上有 $n$ 个点，给定值 $V$ , 有两种移动方式：

走到与当前位置距离不超过 $V$ 的点。

跳到任何一个点，$V$ 变为原先的一半（下取整）。

求从哪些点出发可以到达所有点至少一次。

$n,V\leq2\times10^5$

注意到 $V$ 的取值只有 $O(\log_2V)$ 种，可以表示成如下形式：${2^kV},k\in[-K,0]$考虑状压 DP .

设 $f_S$ 为当 $V$ 的集合为 $S$ 时能走到的前缀长度，同理有 $g_S$ .

预处理从每个位置在某一个 $V$ 的情况下能走到的左右位置就可以快速计算出 $f,g$ 数组了。具体来说就是设 $L_{i,k}$ 为从 $i$ 出发，$v=2^{-k}V$ 时的能到达的最左边的位置；$R_{i,k}$ 数组同理。

最后枚举子集 $s\in S$ , 对于每个子集 $s$ , 可以确保 $L_{g_{S-1},0}$ 到 $R_{f_{\complement_{S}s}}$ 区间内所有点都合法。

给定 $n\times m$ 的四连通黑白棋盘，保证黑色的部分构成森林，有 $q$ 个询问，每次询问一个子矩阵的连通块个数。

$n,m\leq2000,q\leq2\times10^5$

发现这样一个规律：一个子矩阵的连通块个数等于此矩阵中的点数减去边数。

于是预处理二维前缀和，然后 $O(1)$ 询问，总复杂度 $O(nm+q)$ .

预处理边数时需要注意，可以分横边竖边分别统计，横边计算时除去右边一列，竖边计算时除去下边一行。